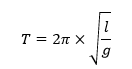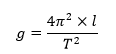E heti kísérletünk során egy olyan jelenséggel fogunk megismerkedni, amely minden anyagnak jellemző tulajdonsága. Ez pedig a tömegvonzás vagy más néven gravitációs erő. Ennek köszönhetően vagyunk képesek a talajon maradni (és nem repülünk el), emiatt kering a Föld a Nap körül, még a saját testünk is rendelkezik valamekkora gravitációs erővel, de ez annyira kicsi, hogy nem érzékelhető.

A gravitáció az anyagok tömegéből eredő kölcsönhatás, amelyet az emberiség már a XVI. század óta vizsgál. Az első jelentős eredmény Galileo Galilei nevéhez köthető, aki a pisai ferde toronyból leejtett golyók segítségével vizsgálta a Föld tömegvonzását. Megállapította, hogy ez minden anyagra egyenlő, tehát egy tollpihére ugyanúgy hat, mint egy vasgolyóra.
Galilei után a XVIII. században Isaac Newtont is foglalkoztatta a kérdés. A legenda szerint egy almafa alatt ülve fejére esett egy alma, és ezek után kezdett el ezzel a témával foglalkozni. Az ő nagy eredménye volt a tömegvonzás képlettel való felírása.
Így ma mi is nagy tudósok nyomdokaiba lépünk és meghatározzuk, mekkora a Föld gravitációs erejéből eredő gyorsulás. Ehhez mindössze egy fonálingára és egy stopperórára lesz szükségünk.
Első lépésként állítsuk össze az ingánkat. Ehhez rögzítsünk fonálon egy kisebb tárgyat olyan helyen, ahol szabadon tud lengeni. Ezután mérjük meg a rögzítés helyétől az ingánk hosszát. Vegyük kézbe a stopperünket, majd óvatosan térítsük ki az ingát. Itt fontos, hogy ne lökjük meg, csak simán engedjük el. Mikor elengedtük, indítsuk el a stoppert is és mérjük meg hogy mennyi idő alatt tér vissza körülbelül háromszor a kiindulási helyére, más szóval mennyi az inga periódusidejének háromszorosa. Azért fontos, hogy ne csak egy lengést mérjünk meg, mert ott nagyon nehéz lenne pontosan megállítani a stoppert. Ettől függetlenül csak egy lengés idejére lesz szükségünk, ezért osszuk el a kapott értéket a lengések számával, esetünkben hárommal.
Ezzel a mérésnek végére is értünk, ezek után már csak a kapott adatokból meg kell határoznunk a gravitációs gyorsulás értékét. Ehhez az inga periódusidejét megadó képletet fogjuk használni.
ahol T az inga periódusideje, l az inga hossza, g pedig a gravitációs gyorsulás értéke. Ebből kifejezzük g-t.
Ide beírva értékeinket, megkaphatjuk a kívánt eredményt.
A kísérletet az alábbi videón tekinthetitek meg:
A gravitációs gyorsulás pontos értéke Magyarországon 9,81 m/s2, melyet gyakran 10 m/s2-re kerekítve használunk. Így nekünk is ehhez közeli eredményt kell kapni a kísérlet elvégzése után.
Ha tetszett a kísérlet, végezzétek el azonos ingahossz mellett más anyagokkal, vagy azonos anyag mellett más ingahosszokkal. Mindegyik esetben hasonló végeredményt kell kapnotok.
Sok sikert és jó szórakozást!
Felhasznált eszközök:
 |
 |
 |
Huttman Balázs
e-mail: fizika@stiefel.hu
Tel.: (1) 415-2010
A kép a http://masseffect.wikia.com/wiki/Earth oldalról származik.